逻辑斯蒂回归模型定义及来源

logist分布

逻辑斯蒂回归模型主要是来源于逻辑斯蒂函数。它有一个大家很熟悉的名字，那就是sigmoid函数：

$f(x) = \frac{1}{1+e^{-x}} \tag1$

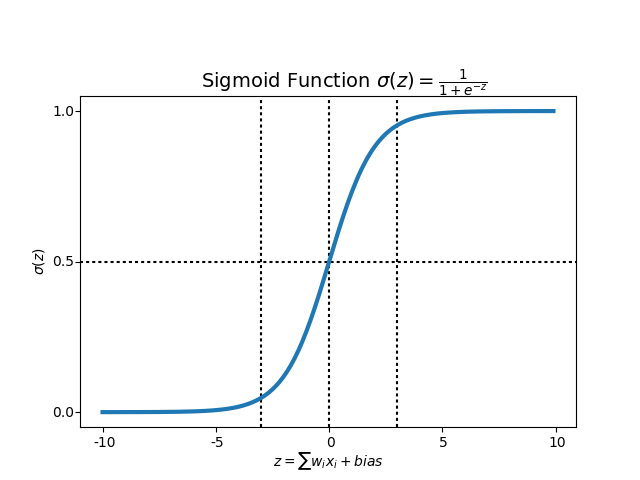
sigmoid函数可以做回归也可以做分类。相比于线性回归，它有一个好处是不容易受极端值的影响。

线性回归

而逻辑斯蒂回归模型模型的另一个则是来源于线性回归：

$g(x) = w_0x_0 + w_1x_1 + ··· + w_nx_n = w^Tx \tag2$

把两者组合起来，对线性回归的结果加上一个逻辑斯蒂函数，就是我们说的逻辑斯蒂回归：

$f(x) = \frac{1}{1+e^{-g(x)}} = \frac{1}{1+e^{-w^Tx}} = \frac{e^{w^Tx}}{1+e^{w^Tx}} \tag3$

logistic回归就是一个线性分类模型，它与线性回归的不同点在于：为了将线性回归输出的很大范围的数，例如从负无穷到正无穷，压缩到0和1之间，这样的输出值表达为“可能性”才能说服广大民众。当然了，把大值压缩到这个范围还有个很好的好处，就是可以消除特别冒尖的变量的影响（不知道理解的是否正确）。而实现这个伟大的功能其实就只需要平凡一举，也就是在输出加一个logistic函数。另外，对于二分类来说，可以简单的认为：如果样本x属于正类的概率大于0.5，那么就判定它是正类，否则就是负类。[1]

逻辑回归的成功之处在于，将原本输出结果范围可以非常大的$w^Tx$ 通过sigmoid函数映射到(0,1)，从而完成概率的估测。

二项逻辑斯蒂回归( binomial logistic regression)模型与推导

二项逻辑斯蒂回归模型

二项回归模型形式表示如下:

$\begin{align} p(Y=1|x)= \frac{e^{w^Tx}}{1+e^{w^Tx}} \tag4\\\ p(Y=0|x)=1−p(Y=1|x)=\frac{1}{1+e^{w^Tx}} \tag5 \end{align}$

在上一节中，我们讲，这个来源于我们的sigmoid函数。而具体的，其实主要来源于一个逻辑斯蒂回归模型。它牵扯到这样一个名词——几率。

一个事件的几率（odds）是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是$p$，那么该事件的几率是$\frac{p}{1-p}$。因次，该事件的对数几率就为：

$logit(p)=log(\frac{p}{1-p}) \tag6$

对逻辑斯蒂回归而言，将$ (4)和(5)带入(6)$得：

$log\frac{P(Y=1|x)}{1-P(Y=1|x)} = w^Tx \tag7$

这个式子就是说，输出Y=1的对数几率是输入x的线性函数。

模型参数估计

首先，我们可以得出似然函数为：

$\prod_{i=1}^N p(Y=1|x_i)^{y_i} p(Y=0|x_i)^{y_i} \tag8$

因为似然函数不好直接求解，所以转换为对数似然函数：

$L(w)= \sum_{i=1}^N [y_ilogp(Y=1|x_i)+(1-y_i)p(Y=0|x_i)] \tag9$

将$ (4)和(5)带入(9)$，很容易求出：

$L(w)= \sum_{i=1}^N[y_i(w^Tx_i)-log((1+e^{w^Tx_i}))] \tag{10}$

对$L(w)$求极大值，就可以得到$w$的估计值。这样，问题就变成了以对数似然函数为目标函数的最优化问题。
这时候，用$L(w)$对$w$求导，得到：

$\begin{align} \nabla_wL(w) = \sum_{i=1}^N(y_ix_i - \frac{e^{w^Tx_i}}{1+e^{w^Tx_i}}x_i) = x_i\sum_{i=1}^N(y_i - h_w(x_i) ) \\\ h_w(x_i) = P(y=1|x_i) \end{align}$

($h_w(x_i)$为逻辑斯蒂模型)

然后我们令该导数为0，你会很失望的发现，它无法解析求解。不信你就去尝试一下。所以没办法了，只能借助高大上的迭代来搞定了。通常采用的方法是梯度下降法或者拟牛顿法。

优化求解

梯度下降(gradient descent)

为了求$L(w)$的极大值，我们采用梯度上升来解决这个问题，即沿着梯度的反向发进行迭代：

$w_{t+1}^T = w_t^T - \alpha\nabla_wL(w) = w_t^T - \alpha\sum_{i=1}^N(y_i - h_w(x_i) )x_i$

其中，参数α叫学习率，就是每一步走多远，这个参数蛮关键的。如果设置的太多，那么很容易就在最优值附加徘徊，因为你步伐太大了。但如果设置的太小，那收敛速度就太慢了，向蜗牛一样，虽然会落在最优的点，但是这速度如果是猴年马月，我们也没这耐心啊。所以有的改进就是在这个学习率这个地方下刀子的。我开始迭代是，学习率大，慢慢的接近最优值的时候，我的学习率变小就可以了。

随机梯度下降SGD (stochastic gradient descent)

梯度下降算法在每次更新回归系数的时候都需要遍历整个数据集（计算整个数据集的回归误差），该方法对小数据集尚可。但当遇到有数十亿样本和成千上万的特征时，就有点力不从心了，它的计算复杂度太高。SGD则是每来一次样本进行一次计算：

$w_{t+1}^T = w_t^T - \alpha(y_i - h_w(x_i) )x_i$

牛顿法

牛顿法简介

此方法用来寻找函数的零点，即$f(x)=0$的根

首先，选择一个接近函数$f(x)$零点的 $x_0$，计算相应的$f(x_0)$和切线斜率 $ f^\prime(x_0) $（这里$f^\prime$表示函数 $f$的导数）。然后我们计算穿过点$ (x_0,f(x_0)) $并且斜率为$ f^\prime(x_0) $的直线和 $x$轴的交点的$x$坐标，也就是求如下方程的解：

$0=(x-x_0)f\prime(x_0) +f(x_0)$

我们将新求得的点的$x$坐标命名为$x_1$，通常 $x_1$会比$x_0$更接近方程$f(x)=0$的解。因此我们现在可以利用 $x_1$开始下一轮迭代。迭代公式可化简为如下所示：

$x_{n+1} = x_n - \frac{f(x_n)}{f^\prime(x_n)}$

牛顿法迭代过程如下所示：

asdfsfd

应用于最优化的牛顿法

在上面介绍的牛顿法中, 通过迭代以求解可微函数$f$的零点的一种算法 (即求 $x$使得$f(x)=0$。
如果我们想要找到函数的最优解（即极值），就需要使函数的导数为零（即求 $x$使得$ f^\prime (x)=0 $）
所以应用于最优化的牛顿法的迭代公式为:

$x_{n+1} = x_n - \frac{f^\prime(x_n)}{f^{\prime\prime}(x_n)}$

根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。[6]

红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。

softmax

参考资料

[1]机器学习算法与Python实践之（七）逻辑回归（Logistic Regression）
[2]统计学习方法——逻辑斯蒂回归模型
[3]【机器学习算法系列之二】浅析Logistic Regression
[4]维基百科：牛顿法
[5]维基百科：应用于最优化的牛顿法
[6]最优化问题中，牛顿法为什么比梯度下降法求解需要的迭代次数更少？ - 大饼土博的回答 - 知乎
[7]Wiki:Multinomial logistic regression
[8]机器学习系列(2)_从初等数学视角解读逻辑回归