拉格朗日乘子法

对拉格朗日乘子法的直观理解

假如你面前有一座山，山上有一条复杂的小路，如果你爬山的时候只能顺着小路走，那么什么时候你发现自己到了某个至高点呢？很明显，当你发现自己不论是往前走，还是往后退时，高度总是下降的，那么这时你就位于一个局部的最高点了。[1]

拉格朗日乘子法的数学原理

经典拉格朗日乘子法是下面的优化问题：

$$\begin{align} \max_{x,y}f(x,y) \\\ s.t.g(x,y)=0 \end{align} \tag 1$$

我们可以将\( f(x,y) \)看作是山，将\( g(x,y)=0 \)看作是山上的小路。

这里采用等高线方式描述\( f(x,y) \)（对方程\( f(x,y)=d \)对不同d绘图），并绘制约束条件\( g(x,y)=0 \)的曲线。相当于约束曲线\( g(x,y)=0 \)与\( f(x,y) \)的某条等高线相切时，取得最优解。(如下图，箭头代表梯度方向)

个人觉得\( g(x,y)=0 \)既可以看作是一条约束直线（紫橘色线），可也以看作是一个平面（蓝色平面）
浅蓝色曲线是橘色线在红色平面上的隐射（也是上图中的红线）
相切指的是紫橘色线在深蓝色平面上与浅蓝色曲线的切点（也是我们要求的极值）

“当\( g(x,y)=0 \)与\( f(x,y) \)等高线相切时”，是取得最优解的充要条件（前提是\( f(x,y) \)是凸函数）。因为没有相切的时候，还可以沿着红线向高的地方前进。该条件可拆分成两部分：

1. \( g(x,y) \)与\( f(x,y) \)的某条等高线相切（等价于寻找使这两个函数梯度方向共线的点）
   （复习课本中梯度的性质：某点梯度的方向就是函数等值线\(f({\bf{x}}) = C\)在这点的法线方向，等值线就是地理的等高线）
2. \( g(x,y)=0 \)

上述条件可用方程组描述如下所示：

$$\begin{cases} \nabla_{x,y}f(x,y) = \lambda \nabla_{x,y} g(x,y) \\\ g(x,y)=0 \end{cases} \tag 2$$

这时引入拉格朗日函数：

$$L(x,y,\lambda) = f(x,y) + \lambda g(x,y) \tag 3$$

则拉格朗日函数\( L(x,y,\lambda) \)：的梯度为

$$\begin{cases} \nabla_{x,y}L(x,y,\lambda) =\nabla_{x,y}f(x,y) + \lambda \nabla_{x,y} g(x,y) \\\ \nabla_{\lambda}L(x,y,\lambda) = g(x,y) \end{cases} \tag 4$$

即若令拉格朗日函数的梯度为零，即令(4)式为零，即可得到方程(2)，虽然\( \lambda \)符号相反但不影响。

系数\( \lambda \)作用

为了消除正负号可能对读者带来的困扰，我们对(2)和(4)做如下变化

$$|\lambda| = |\frac{\nabla f(x)}{\nabla g(x)}| \tag5$$

可以发现，当\( |\lambda| \)越小，\( \nabla g(x) \)的模就越大于\( \nabla f(x) \)。极端情况下，\( |\lambda| \rightarrow 0\)，此时\( |\nabla g(x)| \rightarrow \infty \)。这意味着在\(x\)点，\( g(x) \)几乎是垂直的，对增量非常敏感：当最优值不小心变一点点，条件\( g(x)=0 \)将严重偏离；若\( |\lambda| \)很大，\( g(x) \)几乎是水平的，则其对增量不敏感（若\( g(x) \)的轻微偏离不会造成太大的损失，可以适当牺牲约束条件的精确性，来换取更优的解）。
换句话说，\( |\lambda| \)越小，其求得的结果灵敏度越高，反之越低；可以说\( |\lambda| \)是衡量最优解灵敏度的一种方法。（当然也可以直接求\( \nabla g(x) \)来衡量灵敏度，这样更绝对一点）[2]

例题

设一个具体的例子，我们需要求下列问题[3]:

$$\begin{align} \max_{x,y}f(x,y) = x^2y \\\ s.t.g(x,y)=x^2+y^2-3=0 \end{align}$$

只有一个约束，使用一个乘子，设为\(\lambda\)，列出拉格朗日函数:

$$L(x,,y,\lambda) = f(x,y) - \lambda (g(x,y)-c) =x^2y + \lambda(x^2+y^2-3)$$

接下来求解上式，分别对三个待求量偏微分:

$$\nabla_{x,y,\lambda}L(x,y,\lambda) = (\nabla_x L,\nabla_y L,\nabla_\lambda L)=(2xy+2\lambda x,x^2+2\lambda y,x^2+y^2-3)$$

令偏微分分别等于0，得到:

$$\nabla_{x,y,\lambda}L(x,y,\lambda)=0 \Longleftrightarrow \begin{cases} 2xy+2\lambda x=0\\\ x^2+2\lambda y=0\\\ x^2+y^2-3=0 \end{cases}$$

根据上式，我们可以解得\( (x,y,\lambda) \)为：

$$(\pm\sqrt{2},1,-1);(\pm\sqrt{2},-1,1);(0,\pm\sqrt{3},0)$$

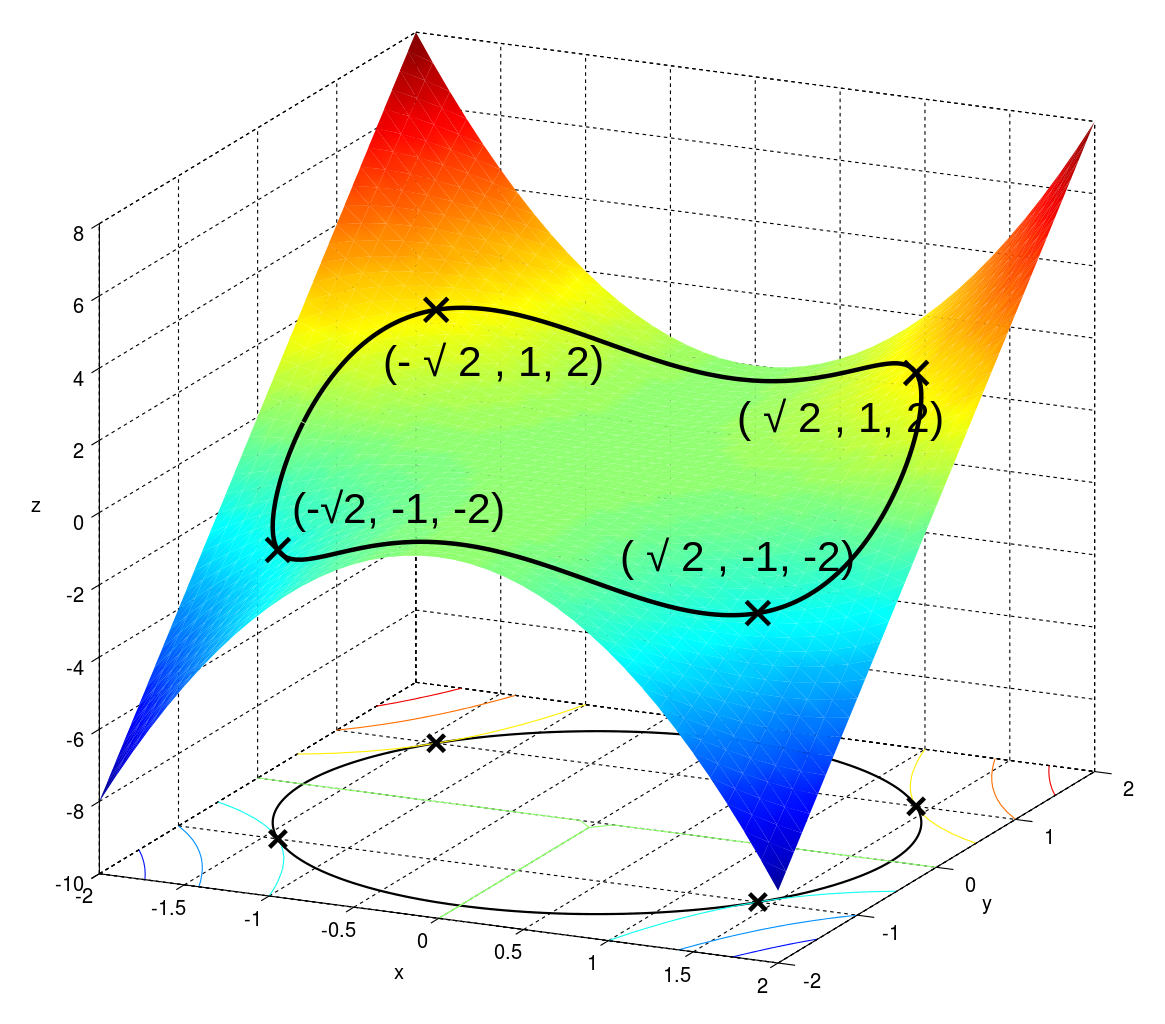
根据几个不同的解带入\( f(x,y) \)得到，2，-2，0，也就是我们需要的最大值，最小值，对应的直观图像解释如上图图所示（非常直观的展现约束和等高线的含义）

参考文献：

[1] 一种对拉格朗日乘子的直观理解
[2] 拉格朗日乘子法（Lagrange Multiplier）详解以及乘子lambda的意义
[3]【直观详解】拉格朗日乘法和KKT条件
[4]浅谈最优化问题的KKT条件