决策树

决策树引导

通俗来说，决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：[5]

女儿：多大年纪了？

母亲：26。

女儿：长的帅不帅？

母亲：挺帅的。

女儿：收入高不？

母亲：不算很高，中等情况。

女儿：是公务员不？

母亲：是，在税务局上班呢。

女儿：那好，我去见见。

这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别：见和不见。假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，那么这个可以用下图表示女孩的决策逻辑（声明：此决策树纯属为了写文章而YY的产物，没有任何根据，也不代表任何女孩的择偶倾向，请各位女同胞莫质问我^_^）：

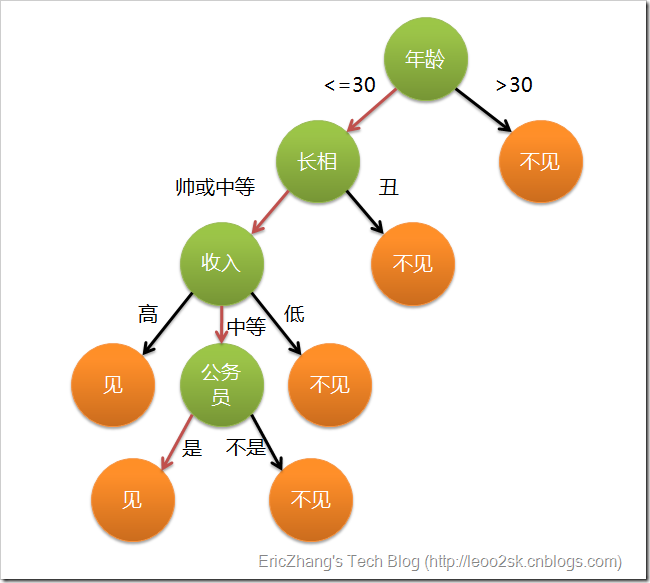
上图完整表达了这个女孩决定是否见一个约会对象的策略，其中绿色节点表示判断条件，橙色节点表示决策结果，箭头表示在一个判断条件在不同情况下的决策路径，图中红色箭头表示了上面例子中女孩的决策过程。

这幅图基本可以算是一颗决策树，说它“基本可以算”是因为图中的判定条件没有量化，如收入高中低等等，还不能算是严格意义上的决策树，如果将所有条件量化，则就变成真正的决策树了。

有了上面直观的认识，我们可以正式定义决策树了：

决策树（decision tree）是一个树结构（可以是二叉树或非二叉树）。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

特征选取

熵

熵的定义

香农把随机变量X的熵值 Η定义如下:

$$H(X)=E[I(X)]=E[-\log(P(X)]$$

其中，P为X的概率质量函数（probability mass function），E为期望函数，而I(X)是X的信息量（又称为自信息），表示包含信息的多少。

当取自有限的样本时，熵的公式可以表示为：

$$H(X)=\sum_i P(x_i)I(x_i)=-\sum_i P(x_i) \log P(x_i)$$

示例

如英语有26个字母，假如每个字母在文章中出现次数平均的话，每个字母的讯息量为：[1]

$$I_e = -\log \frac{1}{26} =4.7$$

以日文五十音平假名作为相对范例，假设每个平假名日语文字在文章中出现的概率相等，每个平假名日语文字可携带的信息量为：

$$I_e = -\log \frac{1}{50} =5.64$$

而汉字常用的有2500个，假如每个汉字在文章中出现次数平均的话，每个汉字的信息量为：

$$I_e = -\log \frac{1}{2500} =11.3$$

实际上每个字母和每个汉字在文章中出现的次数并不平均，比方说较少见字母（如z）和罕用汉字就具有相对高的信息量。但上述计算提供了以下概念：使用书写单元越多的文字，每个单元所包含的讯息量越大。

熵是整个系统的平均消息量。熵越大，随机变量的不确定性就越大，所包含的信息就越多。

$$H=\sum_{i=1}^n p_i I_e = -\sum_{i=1}^n p_i \log_2p_i$$

如果两个系统具有同样大的消息量，如一篇用不同文字写的同一文章，由于汉字的信息量较大，中文文章应用的汉字就比英文文章使用的字母要少。所以汉字印刷的文章要比其他应用总体数量少的字母印刷的文章要短。即使一个汉字占用两个字母的空间，汉字印刷的文章也要比英文字母印刷的用纸少。

条件熵

如果\(H(Y|X=x)\)为变数\(Y\)在变数\(X\)取特定值\(x\)条件下的熵，那么\(H(Y|X)\)就是\(H(Y|X=x)\)在\(X\)取遍所有可能的\(x\)后取平均的结果。[2]

$$\begin{align} H(Y|X) & =\sum_x p(x)H(Y|X=x) \\\ & = -\sum_x p(x) \sum_y p(y|x) \log p(y|x) \\\ & = - \sum_{x,y} p(x,y) \log p(y|x) \\\ & = - \sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)} \\\ & = \sum_{x,y} p(x,y) \log \frac{p(x)}{p(x,y)} \\\ \end{align}$$

当且仅当\(Y\)的值完全由\(X\)确定时\(H(Y|X)=0\)。相反，当且仅当\(Y\)和 \(X\)为独立随机变数时\(H(Y|X)=H(Y)\)。

信息增益

概念

决策树最重要的概念就是信息增益，如果这个概念弄清楚了，那么怎么来选取特征作为决策树的节点就很好理解了。

$$g(Y,X) = H(Y)-H(Y|X)$$

熵\(H(Y)\)：表示随机变量的不确定性。

条件熵\(H(Y|X)\)：在一个条件下，随机变量的不确定性。

信息增益\(g(Y,X)\)：熵 - 条件熵

信息增益在一个条件下，信息不确定性减少的程度

通俗地讲，X(明天下雨)是一个随机变量，X的熵可以算出来， Y(明天阴天)也是随机变量，在阴天情况下下雨的信息熵我们如果也知道的话（此处需要知道其联合概率分布或是通过数据估计）即是条件熵。[3]

两者相减就是信息增益！原来明天下雨例如信息熵是2，条件熵是0.01（因为如果是阴天就下雨的概率很大，信息就少了），这样相减后为1.99，在获得阴天这个信息后，下雨信息不确定性减少了1.99！是很多的！所以信息增益大！也就是说，阴天这个信息对下雨来说是很重要的！

所以在特征选择的时候常常用信息增益，如果IG（信息增益大）的话那么这个特征对于分类来说很关键

例子

我们有如下12组数据：[4]

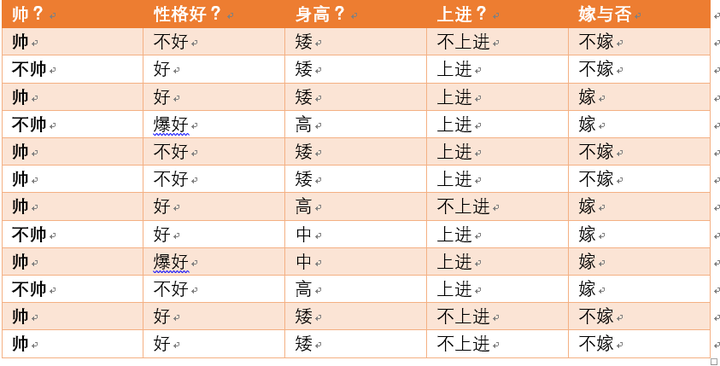
嫁与不嫁的个数为均为6个，占1/2，可以求得随机变量Y（嫁与不嫁）的信息熵为：

$$H(Y=嫁) =-( \frac{1}{2} \log \frac{1}{2} + \frac{1}{2} \log \frac{1}{2} ) = 0.301$$

现在假如我知道了一个男生的身高信息。身高有三个可能的取值{矮，中，高}

矮包括{1,2,3,5,6,11,12}，嫁的个数为1个，不嫁的个数为6个，\( P(Y=嫁|X=矮)=\frac{1}{7} ， P(Y=不嫁|X=矮)=\frac{6}{7} \)

中包括{8,9} ，嫁的个数为2个，不嫁的个数为0个

高包括{4,7,10}，嫁的个数为3个，不嫁的个数为0个

所以：

$$\begin{align} &H(Y|X=矮) =-( \frac{1}{7} \log \frac{1}{7} + \frac{6}{7} \log \frac{6}{7} ) = 0.178 \\\ &H(Y|X=中) = -(1\log1+0) = 0 \\\ &H(Y|X=高) = -(1\log1+0) = 0 \\\ \end{align}$$

又因为

$$p(X = 矮) = \frac{7}{12},p(X =中) = \frac{2}{12},p(X=高) = \frac{3}{12}$$

则可以得出条件熵为

$$H(Y|X) = \frac{7}{12} \times 0.178+ \frac{2}{12} \times 0+\frac{3}{12} \times 0$$

那么我们知道信息熵与条件熵相减就是我们的信息增益，为:

$$0.301-0.103=0.198$$

我们可以知道，本来如果我对一个男生什么都不知道的话，作为他的女朋友决定是否嫁给他的不确定性有0.301这么大。

当我们知道男朋友的身高信息后，不确定度减少了0.198，不确定度只有0.103这么大了，（如果不确定是0就最好了，我肯定嫁给他，因为他好的没有悬念，哈哈）.也就是说，身高这个特征对于我们广大女生同学来说，决定嫁不嫁给自己的男朋友是很重要的。

至少我们知道了身高特征后，我们原来没有底的心里（0.301）已经明朗一半多了，减少0.198了（大于原来的一半了）。

那么这就类似于非诚勿扰节目里面的桥段了，请问女嘉宾，你只能知道男生的一个特征。请问你想知道哪个特征。

假如其它特征我也全算了，信息增益是身高这个特征最大。那么我就可以说，孟非哥哥，我想知道男嘉宾的一个特征是身高特征。因为它在这些特征中，对于我挑夫君是最重要的，信息增益是最大的，知道了这个特征，嫁与不嫁的不确定度减少的是最多的。

信息增益比

以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。使用信息增益比（informatio gain ratio）可以对这一问题进行校正。

$$g_R(Y,X) = \frac{g(Y,X)}{H_X(Y)}$$

决策树的生成

ID3算法

ID3算法就是在每次需要分裂时，计算每个属性的增益率，然后选择增益率最大的属性进行分裂。下面我们继续用SNS社区中不真实账号检测的例子说明如何使用ID3算法构造决策树。为了简单起见，我们假设训练集合包含10个元素：[5]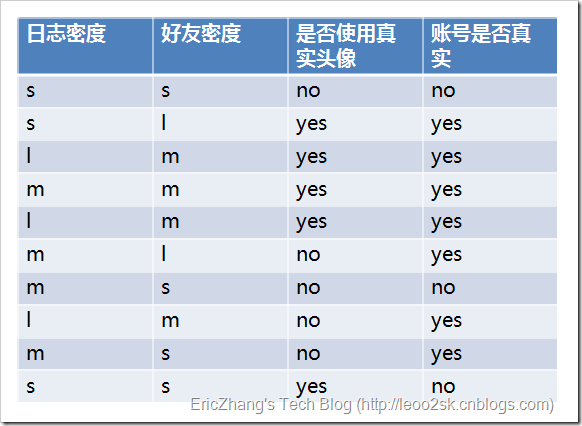

其中s、m和l分别表示小、中和大。

设L、F、H和R表示日志密度、好友密度、是否使用真实头像和账号是否真实，下面计算各属性的信息增益。

$$H(D) = -0.7\log 0.7 -0.3\log 0.3 = 0.879$$ $$H(D|L)=0.3 \times (- \frac{1}{3} \log \frac{1}{3} - \frac{2}{3} \log \frac{2}{3}) +0.4 \times (- \frac{1}{4} \log \frac{1}{4} - \frac{3}{4} \log \frac{3}{4}) + 0.3 \times (- \frac{0}{3} \log \frac{0}{3} - \frac{3}{3} \log \frac{3}{3}) = 0.603$$ $$gain(L) = H(D)-H(D|L)$$

因此日志密度的信息增益是0.276。

用同样方法得到H和F的信息增益分别为0.033和0.553。

因为F具有最大的信息增益，所以第一次分裂选择F为分裂属性，分裂后的结果如下图表示：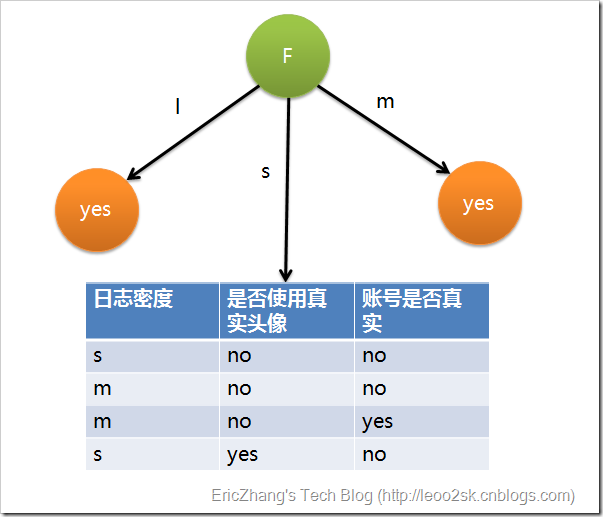

在上图的基础上，再递归使用这个方法计算子节点的分裂属性，最终就可以得到整个决策树。

上面为了简便，将特征属性离散化了，其实日志密度和好友密度都是连续的属性。对于特征属性为连续值，可以如此使用ID3算法：

先将D中元素按照特征属性排序，则每两个相邻元素的中间点可以看做潜在分裂点，从第一个潜在分裂点开始，分裂D并计算两个集合的期望信息，具有最小期望信息的点称为这个属性的最佳分裂点，其信息期望作为此属性的信息期望。

C4.5算法

ID3算法存在一个问题，就是偏向于多值属性，例如，如果存在唯一标识属性ID，则ID3会选择它作为分裂属性，这样虽然使得划分充分纯净，但这种划分对分类几乎毫无用处。ID3的后继算法C4.5使用信息增益比，试图克服这个偏倚。

决策树的剪枝

首先看一看决策树整体的熵：

$$C(T)= \sum_{t=1}^{|T|} N_tH_t(T) = N\sum_{t=1}^{|T|} \frac{N_t}{N}H_t(T) =- N\sum_{t=1}^{|T|} \frac{N_t}{N} \sum_{k=1}^{K} \frac{N_{tk}}{N_t} \log \frac{N_{tk}}{N_t}$$

其中树\(T\)的叶节点个数为\(|T|\)。\(t\)是树\(T\)的叶节点，该叶节点有\(Nt\)个样本点，其中\(k\)类的样本点有\(N{tk}\)个，\(H_t(T)\)表示叶节点的经验熵[7]

其中\(N\)是常数，乘不乘都不影响最终结果。对于离散随机变量X求均值，一般就是pX可能取值，再求和。上面的\(C(T)\)其实就是*不同节点熵的均值呀。为了防止过拟合，就是防止叶节点过多，添加约束项：

损失函数：

$$C_\alpha (T) = C(T)+ \alpha |T|$$

\(C(T）\)表示模型对训练数据的预测误差，即模型与训练数据的拟合程度；\(|T|\)是叶节点的个数，表示模型的复杂度；\(\alpha \geq 0 \)控制两者之间的影响。较大的\(\alpha \)促使选择较简单的模型（树），较小的\(\alpha \)促使选择较复杂的模型（树）。\(\alpha =0\)意味着只考虑与训练数据的拟合程度，不考虑模型的复杂度。[6]

剪枝是决策树学习算法对付“过拟合”的主要手段。剪枝有两种：

预剪枝——在构造过程中，当某个节点满足剪枝条件，则直接停止此分支的构造。

后剪枝——先构造完成完整的决策树，再通过某些条件遍历树进行剪枝。

后剪枝决策树通常比于简直决策树保留了更多的分支。一般情况下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝决策树

CART算法

CART回归树

CART分类树

基尼指数：

$$Gini(p) = \sum_{k=1}^K p_k (1-p_k) = 1- \sum_{k=1}^K p_k^2$$

反应了从数据集随机抽取两样本，标记不一样的概率

CART树剪枝

上节中，得到决策树剪枝的损失函数为：

$$C_\alpha (T) = C(T)+ \alpha |T|$$

对于决策树的某一个内部节点t，以t为单结点树的损失函数是：

$$C_\alpha (t) = C(t)+ \alpha$$

以t为根节点的子树\(T_t\)的损失函数是：

$$C_\alpha(T_t) = C(T_t)+ \alpha |T_t|$$

当\(\alpha=0\) 时及\(\alpha\)从充分小时：

$$C_\alpha(T_t) < C_\alpha (T)$$

当\(\alpha=0 \to \infty\) 时：

$$C_\alpha(T_t) > C_\alpha (T)$$

所以在某一\(\alpha\)有：

$$C_\alpha(T_t) = C_\alpha (T)$$

为了不混淆变量，重新定义：

$$g(t)=\frac{C(t)-C(T_t)}{|T_t|-1}$$

α大于g(t)就是该剪。简而言之：对于同一棵树的结点，α都是一样的，当α从0开始缓慢增大（或者从+∞慢慢减小），总会有某棵子树该剪，其他子树不该剪的情况，即α超过了某个结点的g(t)，但还没有超过其他结点的g(t)。这样随着alpha不断增大，不断地剪枝，就得到了n+1棵子树，接下来只要用独立数据集测试这n+1棵子树，试试哪棵子树的误差最小 就知道那棵是最好的方案了。[6]

参考资料

[1]维基百科：熵 (信息论))
[2]维基百科：条件熵
[3]信息增益到底怎么理解呢？ - Kay Zhou的回答 - 知乎
[4]通俗理解决策树算法中的信息增益 - 忆臻的文章 - 知乎
[5]算法杂货铺——分类算法之决策树(Decision tree)
[6]统计学习方法：CART算法
[7]统计学习方法：决策树（1）
[8]李航 (2012) 统计学习方法. 清华大学出版社, 北京.